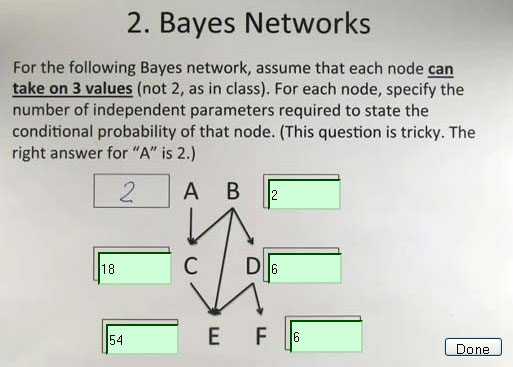
|
This was the second question on final exam and my answers were all correct.
As you can see in the picture, we must say how many independent parameters are required to define each node of the network, but first we must
understand what a Bayes network really is.
Let's consider the simplest of the networks: (A) ---> (B)
This shows that event A is the cause of event B, but Bayes networks are not deterministic, they are probabilistic. This means that
to define this simple network we need a series of probabilities.
First of all some symbol definitions: P(A) is the unconditional probability that A is true. ~A means that A is false and
P(B|A) is the probability that B is true when A is true, otherwise stated it is the probability of B given A.
To define the simple network we need 6 different values: P(A), P(~A), P(B|A), P(~B|A), P(B|~A), P(~B|~A).
However not all 6 parameters are independent. For example, since A can be either true or false and the probabilities are normally expressed
as numbers in the range 0 to 1, we have that P(A)+P(~A)=1 and this means that we can compute one of this values starting from the other.
So for example we have that P(~A)=1-P(A) and so if we want to count the independent parameters needed, for A it is only 1, not 2.
The same applies to the other values, so we have that P(~B|A)=1-P(B|A) and P(~B|~A)=1-P(B|~A).
So the actual independent parameters we need for the whole network is reduced to only 3, for example: P(A), P(B|A), P(B|~A).
The question of the exam was complicated by the fact that each node is defined as tristate. Instead of being only
true or false, each node can have 3 values. Let's call them A1, A2, A3 and B1, B2, B3 and so on. To compute each answer I did the following
(correct) reasonment:
- Node A
- The answer for this node was already given and this clarified any possible doubts for this question. A can have
3 values and the sum of the probabilities is 1: P(A1)+P(A2)+P(A3)=1. So one of the parameters can be computed from the other 2 and we
need a total of 2 independent parameters to define this node.
- Node B
- This node is in the same situation of A, so the same reasonment does apply and we need 2 independent parameters to define it.
- Node C
- This node is influenced by both A and B, so we must first consider all the combinations of the states of A and B. Since
each node can have 3 states, the total of these combinations is 3x3=9. Then, for each of these, we must compute 2 states for C, since the
third value can be computed from the other 2. For example P(C3|A1,B1)=1-P(C1|A1,B1)-P(C2|A1,B1). So we need a total of 9x2=18
independent parameters for this node.
- Node D
- This node depends only on B, so we consider all the states for B and, as before, only 2 states for D. So we need here
3x2=6 parameters.
- Node E
- This is influenced by the nodes B, C and D, so we must compute all the combinations for the states of the parent nodes, which is
3x3x3=27, then for each of these, 2 values for node E. So the total is 27x2=54 independent parameters.
- Node F
- This node is only influenced by another node, so it is the same as for node D and we requires here 6 independent parameters.
|